|
An understanding of how a spring mass system
responds to vibratory influences is helpful in understanding, recognizing and solving many
problems encountered in vibration measurements. In this application note the combined
effects of system mass, stiffness, and damping properties are presented to reveal the
cause and characteristics of resonance.
All machines have three fundamental traits which
combine to determine how the machine will react to excitation forces. These traits are
stiffness K, damping D, and mass M. These traits, actually represent forces inherent to
every machine and structure, tend to resist or oppose vibration.
From an analysis standpoint, it should be remembered that machines, along with their
supporting structures, are complex systems consisting of many spring-mass systems, each
with its own natural frequency. Also, each of these systems may have differing degrees of
freedom with a differing natural frequency. This collection of possible resonant
frequencies, and the many excitation frequencies, all combine to make resonance a very
common problem for the transient vibration analyst. Understanding the basics of how a
system responds to vibratory forces is important to anyone involved in vibration
measurement, analysis, and balancing. From a measurement standpoint, it is important to
remember that every object has a resonant frequency...machinery, pickups, brackets, etc.
Resonance of a pickup mounting bracket, or the pickup itself, will introduce significant
errors to measurements.
Restraining Force
The combined effects of the restraining forces of stiffness, damping, and mass determine
how a system will respond to a given exciting force. Mathematically the relationship is
represented by:
M a + D v + K x Me ω² e sin(ω t - θ)
For simplification, the above equation can be written as:
Mass term + Damping term + Stiffness Term = Restraining Force
The restraining forces, represented by the various terms in the equation, are what
determines how a rotor behaves throughout its operating range. Any excitation force, such
as unbalance, is always in equilibrium with the restraining forces of mass, damping, and
stiffness. The amount of measured vibration, as a result of these combined forces, will
depend upon the combined effect of all three terms in the equation. The phase angle (θ)
change as a rotor increases speed and surpasses a resonance region is dependent upon on
the relationship between the various terms.
Phase Relationship
To understand the phase relationships of the terms, consider that the mass term is
proportional to acceleration, damping term is proportional to velocity, and the stiffness
term is proportional to displacement. In equation form, the acceleration term = -x ω² sin(ω t)
and the velocity term = x ω cos(ω t). Examining the relationship of the acceleration and
velocity equations, a 90 phase difference exists as the terms are integrated. Another
integration produces the stiffness term that is proportional to displacement (x) only, and
the relationship between the stiffness and damping terms have another 90 phase shift.
The effects of frequency (ω) should also be considered along with the phase shifts
noted. Stiffness being proportional to displacement only, and not influenced by frequency,
means that essentially the stiffness term is constant throughout all frequency ranges.
However, the damping and mass terms are influenced by ω and ω², respectively.
Below Resonance
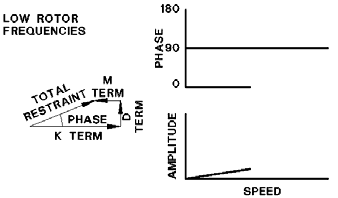 If each of
the individual terms are represented by a vector, and the influences of frequency are
included, the result is a type of graph, similar in shape to a triangle. The figure is a
graphical representation of the relationships of the terms at low frequencies, i.e. slow
rotor speeds. The total restraint vector is the summation of all three vector terms. Note
that the damping and mass terms do not have much influence on the total restraint at low
frequencies, leaving the stiffness term as the dominant term. This means that at
frequencies below the resonance frequency the rotor behaves as a pure spring, sometimes
called a stiff shaft rotor. If each of
the individual terms are represented by a vector, and the influences of frequency are
included, the result is a type of graph, similar in shape to a triangle. The figure is a
graphical representation of the relationships of the terms at low frequencies, i.e. slow
rotor speeds. The total restraint vector is the summation of all three vector terms. Note
that the damping and mass terms do not have much influence on the total restraint at low
frequencies, leaving the stiffness term as the dominant term. This means that at
frequencies below the resonance frequency the rotor behaves as a pure spring, sometimes
called a stiff shaft rotor.
At Resonance
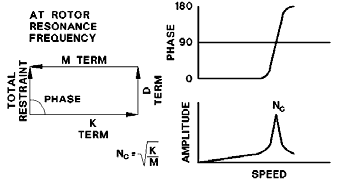 As the rotor
frequency increases, the influence of the damping and mass terms become greater due to the
influence of and in the mass and velocity terms. At a certain frequency the stiffness
and mass terms cancel each other due to the 180 phase difference in the terms. The figure
presents the vectorial relationships and the resultant vibration amplitude response at
resonance condition. As the rotor
frequency increases, the influence of the damping and mass terms become greater due to the
influence of and in the mass and velocity terms. At a certain frequency the stiffness
and mass terms cancel each other due to the 180 phase difference in the terms. The figure
presents the vectorial relationships and the resultant vibration amplitude response at
resonance condition.
When these terms cancel each other the only remaining restraint term is the damping
term to control the system vibration. As the stiffness and mass terms approach the point
of canceling each other, the system's vibration amplitude will increase to a maximum,
constrained only by the available damping from any lubricant present. At resonance the
system has lost the restraining forces of the stiffness and mass terms. A machine
supported by rolling element bearings, which have little or no damping capabilities, will
exhibit a dramatic and sharp increase in vibration amplitude in this region.
This
phenomenon is referred to the resonance frequency or "critical" speed. Operation
in this zone should be avoided since any change in the available damping can have a
dramatic effect upon the measured vibration levels.
Above Resonance
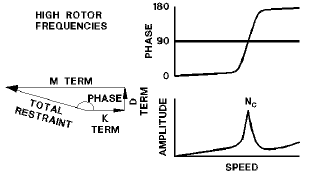 As the rotor
frequency continues to increase, the mass term, which is proportional to ω², becomes the
predominant portion of the total restraint force, growing faster than the other terms. The
figure shows the vector representation of the forces and the vibration amplitude at high
rotor frequencies. Note that as speed increases further the phase angle change approaches
another 90° shift. The rotor behaves as a pure mass with little impact from the constant
stiffness term and the relatively slowly changing damping term. A rotor operating in this
region is called a flexible rotor since it rotates around its mass centerline, not its
geometric centerline. As the rotor
frequency continues to increase, the mass term, which is proportional to ω², becomes the
predominant portion of the total restraint force, growing faster than the other terms. The
figure shows the vector representation of the forces and the vibration amplitude at high
rotor frequencies. Note that as speed increases further the phase angle change approaches
another 90° shift. The rotor behaves as a pure mass with little impact from the constant
stiffness term and the relatively slowly changing damping term. A rotor operating in this
region is called a flexible rotor since it rotates around its mass centerline, not its
geometric centerline.
Thus, as rotor frequencies increase, three regions are found where one of the component
terms is dominant over the other two terms. The summation of the three terms is
represented by the vector labeled: Total Restraint. The total restraint vector is what is
measured as vibration amplitude and its associated phase angle. As the rotor speed passes
through each of these regions the measured phase angle will change by 90° and will exhibit
an overall phase shift of 180° as it surpasses a critical "resonance" speed:
Nc.
|

